Y 1 4x graph. Algorithm para sa pagbuo ng isang quadratic function. Mga benepisyo ng online charting
"Natural na logarithm" - 0.1. Natural logarithms. 4. Logarithmic darts. 0.04. 7.121.
"Power function grade 9" - U. Cubic parabola. Y = x3. Ang guro ng ika-9 na baitang Ladoshkina I.A. Y = x2. Hyperbola. 0. Y = xn, y = x-n kung saan ang n ay isang ibinigay na natural na numero. X. Ang exponent ay isang natural na numero (2n).
"Quadratic Function" - 1 Depinisyon quadratic function 2 Mga katangian ng isang function 3 Mga graph ng isang function 4 Quadratic inequalities 5 Konklusyon. Mga Katangian: Hindi pagkakapantay-pantay: Inihanda ng 8A class student na si Andrey Gerlitz. Plano: Graph: -Mga agwat ng monotonicity para sa isang > 0 para sa a< 0. Квадратичная функция. Квадратичные функции используются уже много лет.
“Quadratic function and its graph” - Solution.y=4x A(0.5:1) 1=1 A- belongs. Kapag a=1, ang formula na y=ax ay nasa anyo.
"8th grade quadratic function" - 1) Buuin ang vertex ng isang parabola. Pag-plot ng isang graph ng isang quadratic function. x. -7. Bumuo ng isang graph ng function. Algebra 8th grade Teacher 496 Bovina school T.V. -1. Plano sa pagtatayo. 2) Buuin ang axis ng symmetry x=-1. y.
Bumuo ng curve na ibinigay ng mga parametric equation\
Suriin muna natin ang mga graph ng mga function na \(x\left(t \right)\) at \(x\left(t \right)\). Ang parehong mga function ay mga cubic polynomial na tinukoy para sa lahat ng \(x \in \mathbb(R).\) Hanapin ang derivative \(x"\left(t \right):\) \[ (x"\left(t \ kanan) = (\left(((t^3) + (t^2) - t) \right)^\prime ) ) = (3(t^2) + 2t - 1.) \] Paglutas ng equation \ ( x"\left(t \right) = 0,\) tinutukoy namin ang mga nakatigil na punto ng function \(x\left(t \right):\) \[ (x"\left(t \right) = 0 ,)\;\ ; (\Rightarrow 3(t^2) + 2t - 1 = 0,)\;\; (\Rightarrow (t_(1,2)) = \frac(( - 2 \pm \sqrt (16) ))(6) = - 1;\;\frac(1)(3).) \] Kapag \ (t = 1\) ang function na \(x\left(t \right)\) ay umabot sa maximum na katumbas ng \ at sa puntong \(t = \large\frac(1)(3)\normalsize\) mayroon ito isang minimum na katumbas ng \[ (x\left((\frac(1)(3)) \right) ) = ((\left((\frac(1)(3)) \right)^3) + (\ kaliwa((\ frac(1)(3)) \right)^2) - \left((\frac(1)(3)) \right) ) = (\frac(1)((27)) + \ frac(1) (9) - \frac(1)(3) = - \frac(5)((27)).) \] Isaalang-alang ang derivative \(y"\left(t \right):\) \ [ (y"\ left(t \right) = (\left(((t^3) + 2(t^2) - 4t) \right)^\prime ) ) = (3(t^2) + 4t - 4.) \ ] Hanapin ang mga nakatigil na punto ng function \(y\left(t \right):\) \[ (y"\left(t \right) = 0,)\;\; (\Rightarrow 3 (t^2) + 4t - 4 = 0,)\;\; (\Rightarrow (t_(1,2)) = \frac(( - 4 \pm \sqrt (64) ))(6) = - 2 ;\;\frac(2) (3).) \] Dito, sa katulad na paraan, ang function na \(y\left(t \right)\) ay umaabot sa maximum sa puntong \(t = -2:\) \ at isang minimum sa puntong \(t = \large\frac (2)(3)\normalsize:\) \[ (y\left((\frac(2)(3)) \right) ) = ((\left ((\frac(2)(3)) \right )^3) + 2(\left((\frac(2)(3)) \right)^2) - 4 \cdot \frac(2)(3 ) ) = (\frac(8)((27) ) + \frac(8)(9) - \frac(8)(3) ) = ( - \frac((40))((27)).) \] Ang mga graph ng mga function \(x\left(t \right )\), \(y\left(t \right)\) ay ipinapakita sa eskematiko sa Figure \(15a.\)
Fig.15a |
Fig.15b |
Fig.15c |
Tandaan na dahil \[ (\lim\limits_(t \to \pm \infty ) x\left(t \right) = \pm \infty ,)\;\;\; (\lim\limits_(t \to \pm \infty ) y\left(t \right) = \pm \infty ,) \] pagkatapos ay ang curve \(y\left(x \right)\) ay walang vertical, walang pahalang na asymptotes. Bukod dito, dahil \[ (k = \lim\limits_(t \to \pm \infty ) \frac((y\left(t \right)))((x\left(t \right))) ) = ( \lim\limits_(t \to \pm \infty ) \frac(((t^3) + 2(t^2) - 4t))(((t^3) + (t^2) - t) ) ) = (\lim\limits_(t \to \pm \infty ) \frac((1 + \frac(2)(t) - \frac(4)(((t^2)))))(( 1 + \frac(1)(t) - \frac(1)(((t^2))))) = 1,) \] \[ (b = \lim\limits_(t \to \pm \infty ) \left[ (y\left(t \right) - kx\left(t \right)) \right] ) = (\lim\limits_(t \to \pm \infty ) \left((\cancel(\ color (asul)(t^3)) + \color(pula)(2(t^2)) - \color(berde)(4t) - \cancel(\color(blue)(t^3)) - \ color (pula)(t^2) + \color(berde)(t)) \kanan) ) = (\lim\limits_(t \to \pm \infty ) \left((\color(red)(t^ 2 ) - \color(green)(3t)) \right) = + \infty ,) \] pagkatapos ay ang curve \(y\left(x \right)\) ay wala ring oblique asymptotes.
Tukuyin natin ang mga intersection point ng graph \(y\left(x \right)\) gamit ang mga coordinate axes. Ang intersection sa x-axis ay nangyayari sa mga sumusunod na punto: \[ (y\left(t \right) = (t^3) + 2(t^2) - 4t = 0,)\;\; (\Rightarrow t\left(((t^2) + 2t - 4) \right) = 0;) \]
\(((t^2) + 2t - 4 = 0,)\;\; (\Rightarrow D = 4 - 4 \cdot \left((- 4) \right) = 20,)\;\; (\ Rightarrow (t_(2,3)) = \malaki\frac(( - 2 \pm \sqrt (20) ))(2)\normalsize = - 1 \pm \sqrt 5 .) \)
\(((t^2) + t - 1 = 0,)\;\; (\Rightarrow D = 1 - 4 \cdot \left(( - 1) \right) = 5,)\;\; (\ Rightarrow (t_(2,3)) = \large\frac(( - 1 \pm \sqrt (5) ))(2)\normalsize.) \)
Sa ikalawang pagitan \(\left(( - 2, - 1) \right)\) ang variable na \(x\) ay tumataas mula sa \(x\left(( - 2) \right) = - 2\) hanggang \ (x \left(( - 1) \right) = 1,\) at ang variable na \(y\) ay bumababa mula sa \(y\left((- 2) \right) = 8\) hanggang \(y\left (( - 1) \right) = 5.\) Narito mayroon kaming isang seksyon ng isang bumababa na kurba \(y\left(x \right).\) Nag-intersect ito sa ordinate axis sa puntong \(\left((0.3). + 2\sqrt 5 ) \kanan).\)
Sa ikatlong pagitan \(\left(( - 1,\large\frac(1)(3)\normalsize) \right)\) parehong bumababa ang mga variable. Ang halaga ng \(x\) ay nagbabago mula sa \(x\left(( - 1) \right) = 1\) patungong \(x\left((\large\frac(1)(3)\normalsize) \right ) = - \large\frac(5)((27))\normalsize.\) Alinsunod dito, ang halaga ng \(y\) ay bumababa mula sa \(y\left(( - 1) \right) = 5\) hanggang \(y\ left((\large\frac(1)(3)\normalsize) \right) = - \large\frac(29)((27))\normalsize.\) Curve \(y\left(x \right)\ ) intersects ang pinagmulan ng mga coordinate.
Sa ikaapat na pagitan \(\left((\large\frac(1)(3)\normalsize,\large\frac(2)(3)\normalsize) \right)\) ang variable na \(x\) ay tumataas mula sa \( x\left((\large\frac(1)(3)\normalsize) \right) = - \large\frac(5)((27))\normalsize\) to \(x\left((\ large\ frac(2)(3)\normalsize) \right) = \large\frac(2)((27))\normalsize,\) at ang variable na \(y\) ay bumababa mula sa \(y\left(( \large\ frac(1)(3)\normalsize) \right) = - \large\frac(29)((27))\normalsize\) hanggang \(y\left((\large\frac(2)( 3)\ normalsize) \right) = - \large\frac(40)((27))\normalsize.\) Sa seksyong ito, ang curve \(y\left(x \right)\) ay nag-intersect sa ordinate axis sa point \(\left( (0.3 - 2\sqrt 5 ) \right).\)
Sa wakas, sa huling interval \(\left((\large\frac(2)(3)\normalsize, + \infty ) \right)\) parehong function \(x\left(t \right)\), \ ( y\left(t \right)\) tumaas. Ang curve \(y\left(x \right)\) ay nag-intersect sa x-axis sa puntong \(x = - 9 + 5\sqrt 5 \approx 2.18.\)
Upang linawin ang hugis ng curve \(y\left(x \right)\), kalkulahin natin ang maximum at minimum na mga puntos. Ang derivative na \(y"\left(x \right)\) ay ipinahayag bilang \[ (y"\left(x \right) = (y"_x) ) = (\frac(((y"_t))) (((x"_t))) ) = (\frac((((\left(((t^3)) + 2(t^2) - 4t) \right))^\prime )))((( ( \left(((t^3) + (t^2) - t) \right))^\prime ))) ) = (\frac((3(t^2) + 4t - 4))(( 3 (t^2) + 2t - 1)) ) = (\frac((\cancel(3)\left((t + 2) \right)\left((t - \frac(2)(3)) \ kanan)))((\kanselahin(3)\kaliwa((t + 1) \kanan)\kaliwa((t - \frac(1)(3)) \kanan))) ) = (\frac(( \ kaliwa((t + 2) \kanan)\kaliwa((t - \frac(2)(3)) \kanan)))(\kaliwa((t + 1) \kanan)\kaliwa((t - \ frac(1)(3)) \right))).) \] Ang pagbabago sa sign ng derivative na \(y"\left(x \right)\) ay ipinapakita sa Figure \(15c.\) Maaari itong makikita na sa puntong \(t = - 2,\) i.e. sa hangganan ng \(I\)-th at \(II\)-th na pagitan ang curve ay may maximum, at sa \(t = \large\frac(2)(3)\normalsize\) (sa hangganan ng \(IV\) ika at \(V\)th na pagitan) mayroong pinakamababa. Kapag dumadaan sa puntong \(t = \large\frac(1)(3)\normalsize\), binabago din ng derivative ang sign mula plus hanggang minus, ngunit sa rehiyong ito ang curve \(y\left(x \right) \) ay hindi isang natatanging function. Samakatuwid, ang ipinahiwatig na punto ay hindi isang extremum.
Sinusuri din namin ang convexity ng curve na ito. Pangalawang derivative Ang \(y""\left(x \right)\) ay may anyo: \[ y""\left(x \right) = (y""_(xx)) = \frac((((\left( ( (y"_x)) \right))"_t)))(((x"_t))) = \frac((((\left((\frac((3(t^2)))) + 4t - 4) ) )((3(t^2) + 2t - 1))) \kanan))^\prime )))(((\kaliwa(((t^3)) + (t^2) - t) \ kanan ))^\prime ))) = \frac((\left((6t + 4) \right)\left((3(t^2) + 2t - 1) \right) - \left((3( t ^2) + 4t - 4) \kanan)\kaliwa((6t + 2) \kanan)))(((\kaliwa((3(t^2)) + 2t - 1) \kanan))^3 ) )) = \frac((18(t^3) + 12(t^2) + 12(t^2) + 8t - 6t - 4 - \left((18(t^3) + 24(t^ 2 ) - 24t + 6(t^2) + 8t - 8) \kanan)))((((\kaliwa((3(t^2)) + 2t - 1) \kanan))^3))) = \ frac((\cancel(\color(blue)(18(t^3))) + \color(red)(24(t^2)) + \color(berde)(2t) - \color(maroon) ( 4) - \cancel(\color(blue)(18(t^3))) - \color(red)(30(t^2)) + \color(green)(16t) + \color(maroon) ( 8)))((((\kaliwa((3(t^2)) + 2t - 1) \right))^3))) = \frac(( - \color(pula)(6(t^2) ) ) + \color(berde)(18t) + \color(maroon)(4)))((((\kaliwa((3(t^2)) + 2t - 1) \kanan))^3))) = \frac(( - 6\left((t - \frac((9 - \sqrt (105) ))(6)) \right)\left((t - \frac((9 + \sqrt (105)) ) )(6)) \kanan)))((((\kaliwa((t + 1) \kanan))^3)((\kaliwa((3t - 1) \kanan))^3))). \] Dahil dito, binabago ng pangalawang derivative ang sign nito sa kabaligtaran kapag dumadaan sa mga sumusunod na punto (Fig.\(15с\)): \[ ((t_1) = - 1:\;\;x\left(( - 1) ) \right ) = 1,)\;\; (y\left(( - 1) \right) = 5;) \] \[ ((t_2) = \frac((9 - \sqrt (105) ))(6):)\;\; (x\left((\frac((9 - \sqrt (105) ))(6)) \right) \approx 0.24;)\;\; (y\left((\frac((9 - \sqrt (105) ))(6)) \right) \approx 0.91;) \] \[ ((t_3) = \frac(1)(3) :) \;\; (x\left((\frac(1)(3)) \right) = - \frac(5)((27)),)\;\; (y\left((\frac(1)(3)) \right) = - \frac((29))((27));) \] \[ ((t_4) = \frac((9 + \ sqrt (105) ))(6):)\;\; (x\left((\frac((9 + \sqrt (105) ))(6)) \right) \approx 40.1;)\;\; (y\left((\frac((9 + \sqrt (105) ))(6)) \right) \approx 40.8.) \] Samakatuwid, ang mga ipinahiwatig na punto ay kumakatawan sa mga inflection point ng curve \(y\left( x \kanan).\)
Ang isang schematic graph ng curve \(y\left(x \right)\) ay ipinapakita sa itaas sa Figure \(15b.\)
Magplano para sa pagbuo ng isang quadratic function.
1. Function domain (D(y)).
2. Ang graph ng function na ito ay isang parabola, ang mga sanga nito ay nakadirekta paitaas (pababa), dahil a = __ > 0 (a = __< 0).
3. Mga coordinate ng vertex ng parabola.
4. Equation ng axis ng symmetry.
5. Punto ng intersection ng graph sa axisOY.
6. Mga function na zero.
7. Talaan ng mga halaga ng function.
8. Iskedyul.
Halimbawa ng paglalagay ng isang function y = x 2 – 4 x + 3
1. D(y) = (- ∞; + ∞).
2. Ang graph ng function na ito ay isang parabola, ang mga sanga nito ay nakadirekta paitaas, dahil a = 1 > 0.
3. Mga coordinate ng vertex ng parabola:
x 0 = - , y 0 = 2 2 - 4 2 + 3 = 4 – 8 + 3 = - 1.
4. Equation ng axis ng symmetryx = 2.
5. Punto ng intersection sa axisOY (0; 3).
6. Mga function na zero:
x 2 – 4 x + 3 = 0 D = (- 4) 2 – 4 1 3 = 16 -12 = 4 = 2 2
x 1 = = 1 x 2 = = 3
7. Gumawa tayo ng talahanayan ng mga halaga ng function:
0
1
2
3
3
0
- 1
0
8. Bumuo tayo ng graph

Mga katangian ng function:
1. Set ng mga halaga ng function (E (y)).
2. Mga agwat ng patuloy na pag-sign ng function (y>0, y<0).
3. Mga agwat ng monotonicity ng isang function (tumataas, bumababa).
4. Mga puntos ng maximum at minimum ng function.
Mga katangian ng pag-andar y = x 2 – 4 x + 3.

1. E (y) = [-1; + ∞).
2. y < 0, при x (1; 3).
Ang pagbuo ng mga graph ng mga function na naglalaman ng mga module ay kadalasang nagdudulot ng malaking kahirapan para sa mga mag-aaral. Gayunpaman, ang lahat ay hindi masyadong masama. Ito ay sapat na upang matandaan ang ilang mga algorithm para sa paglutas ng mga naturang problema, at maaari mong madaling bumuo ng isang graph ng kahit na ang pinaka tila kumplikadong function. Alamin natin kung anong uri ng mga algorithm ito.
1. Pag-plot ng graph ng function na y = |f(x)|
Tandaan na ang hanay ng mga halaga ng function y = |f(x)| : y ≥ 0. Kaya, ang mga graph ng naturang mga function ay palaging ganap na matatagpuan sa itaas na kalahating eroplano.
Pag-plot ng graph ng function na y = |f(x)| ay binubuo ng sumusunod na simpleng apat na hakbang.
1) Maingat at maingat na bumuo ng isang graph ng function na y = f(x).
2) Iwanang hindi nagbabago ang lahat ng punto sa graph na nasa itaas o sa 0x axis.
3) Ipakita ang bahagi ng graph na nasa ibaba ng 0x axis na simetriko na nauugnay sa 0x axis.
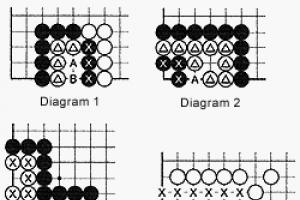
Halimbawa 1. Gumuhit ng graph ng function na y = |x 2 – 4x + 3|
1) Bumubuo kami ng graph ng function na y = x 2 – 4x + 3. Malinaw, ang graph ng function na ito ay isang parabola. Hanapin natin ang mga coordinate ng lahat ng mga punto ng intersection ng parabola na may mga coordinate axes at mga coordinate ng vertex ng parabola.
x 2 – 4x + 3 = 0.
x 1 = 3, x 2 = 1.
Samakatuwid, ang parabola ay nag-intersect sa 0x axis sa mga punto (3, 0) at (1, 0).
y = 0 2 – 4 0 + 3 = 3.
Samakatuwid, ang parabola ay nag-intersect sa 0y axis sa punto (0, 3).
Mga coordinate ng parabola vertex:
x sa = -(-4/2) = 2, y sa = 2 2 – 4 2 + 3 = -1.
Samakatuwid, ang punto (2, -1) ay ang vertex ng parabola na ito.
Gumuhit ng parabola gamit ang nakuhang datos (Larawan 1)
2) Ang bahagi ng graph na nasa ibaba ng 0x axis ay ipinapakita nang simetriko na nauugnay sa 0x axis.
3) Kumuha kami ng graph ng orihinal na function ( kanin. 2, ipinapakita sa may tuldok na linya).

2. Pag-plot ng function na y = f(|x|)
Tandaan na ang mga function ng anyong y = f(|x|) ay pantay:
y(-x) = f(|-x|) = f(|x|) = y(x). Nangangahulugan ito na ang mga graph ng naturang mga function ay simetriko tungkol sa 0y axis.
Ang pag-plot ng graph ng function na y = f(|x|) ay binubuo ng sumusunod na simpleng chain of actions.
1) I-graph ang function na y = f(x).
2) Iwanan ang bahaging iyon ng graph kung saan ang x ≥ 0, iyon ay, ang bahagi ng graph na matatagpuan sa kanang kalahating eroplano.
3) Ipakita ang bahagi ng graph na tinukoy sa punto (2) nang simetriko sa 0y axis.
4) Bilang panghuling graph, piliin ang unyon ng mga kurba na nakuha sa mga puntos (2) at (3).
Halimbawa 2. Gumuhit ng graph ng function na y = x 2 – 4 · |x| + 3
Dahil x 2 = |x| 2, pagkatapos ay ang orihinal na function ay maaaring muling isulat sa sumusunod na anyo: y = |x| 2 – 4 · |x| + 3. Ngayon ay maaari nating ilapat ang algorithm na iminungkahi sa itaas.
1) Maingat at maingat tayong bumuo ng graph ng function na y = x 2 – 4 x + 3 (tingnan din kanin. 1).
2) Iniiwan namin ang bahaging iyon ng graph kung saan ang x ≥ 0, iyon ay, ang bahagi ng graph na matatagpuan sa kanang kalahating eroplano.
3) Ipakita ang kanang bahagi ng graph nang simetriko sa 0y axis.
(Larawan 3).

Halimbawa 3. Gumuhit ng graph ng function na y = log 2 |x|
Inilapat namin ang scheme na ibinigay sa itaas.
1) Bumuo ng graph ng function na y = log 2 x (Larawan 4).
3. Pag-plot ng function na y = |f(|x|)|
Tandaan na ang mga function ng form na y = |f(|x|)| ay pantay din. Sa katunayan, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), at samakatuwid, ang kanilang mga graph ay simetriko tungkol sa 0y axis. Ang hanay ng mga halaga ng naturang mga pag-andar: y ≥ 0. Nangangahulugan ito na ang mga graph ng naturang mga function ay ganap na matatagpuan sa itaas na kalahating eroplano.
Upang i-plot ang function na y = |f(|x|)|, kailangan mong:
1) Maingat na bumuo ng graph ng function na y = f(|x|).
2) Iwanang hindi nagbabago ang bahagi ng graph na nasa itaas o sa 0x axis.
3) Ipakita ang bahagi ng graph na matatagpuan sa ibaba ng 0x axis na simetriko na nauugnay sa 0x axis.
4) Bilang panghuling graph, piliin ang unyon ng mga kurba na nakuha sa mga puntos (2) at (3).
Halimbawa 4. Gumuhit ng graph ng function na y = |-x 2 + 2|x| – 1|.
1) Tandaan na x 2 = |x| 2. Nangangahulugan ito na sa halip na ang orihinal na function y = -x 2 + 2|x| - 1
maaari mong gamitin ang function na y = -|x| 2 + 2|x| – 1, dahil magkasabay ang kanilang mga graph.
Bumubuo kami ng graph na y = -|x| 2 + 2|x| – 1. Para dito ginagamit namin ang algorithm 2.
a) I-graph ang function na y = -x 2 + 2x – 1 (Larawan 6).

b) Iniiwan namin ang bahaging iyon ng graph na matatagpuan sa kanang kalahating eroplano.
c) Ipinapakita namin ang resultang bahagi ng graph nang simetriko sa 0y axis.
d) Ang resultang graph ay ipinapakita sa may tuldok na linya sa figure (Larawan 7).

2) Walang mga punto sa itaas ng 0x axis; iniiwan namin ang mga puntos sa 0x axis na hindi nagbabago.
3) Ang bahagi ng graph na matatagpuan sa ibaba ng 0x axis ay ipinapakita sa simetriko na nauugnay sa 0x.
4) Ang resultang graph ay ipinapakita sa figure na may tuldok na linya (Larawan 8).

Halimbawa 5. I-graph ang function na y = |(2|x| – 4) / (|x| + 3)|
1) Una kailangan mong i-plot ang function na y = (2|x| – 4) / (|x| + 3). Upang gawin ito, bumalik kami sa Algorithm 2.
a) Maingat na i-plot ang function na y = (2x – 4) / (x + 3) (Larawan 9).

Tandaan na ang function na ito ay fractional linear at ang graph nito ay hyperbola. Upang mag-plot ng curve, kailangan mo munang hanapin ang mga asymptotes ng graph. Pahalang – y = 2/1 (ang ratio ng mga coefficient ng x sa numerator at denominator ng fraction), patayo – x = -3.
2) Iiwan namin ang bahaging iyon ng graph na nasa itaas ng 0x axis o dito na hindi nagbabago.
3) Ang bahagi ng graph na matatagpuan sa ibaba ng 0x axis ay ipapakita sa simetriko na nauugnay sa 0x.
4) Ang huling graph ay ipinapakita sa figure (Larawan 11).
website, kapag kumukopya ng materyal nang buo o bahagi, kinakailangan ang isang link sa pinagmulan.
Paano gumawa ng parabola? Mayroong ilang mga paraan upang i-graph ang isang quadratic function. Ang bawat isa sa kanila ay may mga kalamangan at kahinaan. Isaalang-alang natin ang dalawang paraan.
Magsimula tayo sa pamamagitan ng pag-plot ng quadratic function ng anyong y=x²+bx+c at y= -x²+bx+c.
Halimbawa.
I-graph ang function na y=x²+2x-3.
Solusyon:
Ang y=x²+2x-3 ay isang quadratic function. Ang graph ay isang parabola na may mga sanga sa itaas. Mga coordinate ng parabola vertex
![]()
Mula sa vertex (-1;-4) bumuo kami ng isang graph ng parabola y=x² (bilang mula sa pinagmulan ng mga coordinate. Sa halip na (0;0) - vertex (-1;-4). Mula sa (-1; -4) pumunta kami sa kanan ng 1 unit at pataas ng 1 unit, pagkatapos ay kaliwa ng 1 at pataas ng 1; higit pa: 2 - kanan, 4 - pataas, 2 - kaliwa, 4 - pataas; 3 - kanan, 9 - pataas, 3 - kaliwa, 9 - pataas. Kung hindi sapat ang 7 puntos na ito, 4 sa kanan, 16 sa itaas, atbp.).

Ang graph ng quadratic function na y= -x²+bx+c ay isang parabola, na ang mga sanga nito ay nakadirekta pababa. Upang makabuo ng isang graph, hinahanap namin ang mga coordinate ng vertex at mula dito ay bumubuo kami ng isang parabola y= -x².
Halimbawa.
I-graph ang function na y= -x²+2x+8.
Solusyon:
y= -x²+2x+8 ay isang quadratic function. Ang graph ay isang parabola na may mga sanga pababa. Mga coordinate ng parabola vertex
![]()
Mula sa itaas ay bumuo kami ng parabola y= -x² (1 - sa kanan, 1- pababa; 1 - kaliwa, 1 - pababa; 2 - kanan, 4 - pababa; 2 - kaliwa, 4 - pababa, atbp.):

Ang pamamaraang ito ay nagbibigay-daan sa iyo na bumuo ng isang parabola nang mabilis at hindi nagdudulot ng mga kahirapan kung alam mo kung paano i-graph ang mga function na y=x² at y= -x². Disadvantage: kung ang mga coordinate ng vertex ay mga fractional na numero, hindi masyadong maginhawa upang bumuo ng isang graph. Kung kailangan mong malaman ang eksaktong mga halaga ng mga punto ng intersection ng graph na may Ox axis, kakailanganin mong dagdagan ang paglutas ng equation na x²+bx+c=0 (o -x²+bx+c=0), kahit na ang mga puntong ito ay maaaring direktang matukoy mula sa pagguhit.
Ang isa pang paraan upang bumuo ng isang parabola ay sa pamamagitan ng mga puntos, iyon ay, maaari kang makahanap ng ilang mga punto sa graph at gumuhit ng isang parabola sa pamamagitan ng mga ito (isinasaalang-alang na ang linyang x=xₒ ay ang axis ng symmetry nito). Kadalasan para dito ay kinukuha nila ang vertex ng parabola, ang mga punto ng intersection ng graph na may mga coordinate axes at 1-2 karagdagang puntos.
Gumuhit ng graph ng function na y=x²+5x+4.
Solusyon:
Ang y=x²+5x+4 ay isang quadratic function. Ang graph ay isang parabola na may mga sanga sa itaas. Mga coordinate ng parabola vertex
![]()
ibig sabihin, ang vertex ng parabola ay ang punto (-2.5; -2.25).
Naghahanap ng . Sa punto ng intersection sa Ox axis y=0: x²+5x+4=0. Ang mga ugat ng quadratic equation x1=-1, x2=-4, iyon ay, nakakuha kami ng dalawang puntos sa graph (-1; 0) at (-4; 0).
Sa punto ng intersection ng graph na may Oy axis x=0: y=0²+5∙0+4=4. Nakuha namin ang punto (0; 4).
Upang linawin ang graph, makakahanap ka ng karagdagang punto. Kunin natin ang x=1, pagkatapos ay y=1²+5∙1+4=10, ibig sabihin, ang isa pang punto sa graph ay (1; 10). Minarkahan namin ang mga puntong ito sa coordinate plane. Isinasaalang-alang ang simetrya ng parabola na nauugnay sa linya na dumadaan sa tuktok nito, minarkahan namin ang dalawa pang puntos: (-5; 6) at (-6; 10) at gumuhit ng parabola sa pamamagitan ng mga ito:

I-graph ang function na y= -x²-3x.
Solusyon:
Ang y= -x²-3x ay isang quadratic function. Ang graph ay isang parabola na may mga sanga pababa. Mga coordinate ng parabola vertex
![]()
Ang vertex (-1.5; 2.25) ay ang unang punto ng parabola.
Sa mga punto ng intersection ng graph na may x-axis y=0, iyon ay, nalulutas namin ang equation -x²-3x=0. Ang mga ugat nito ay x=0 at x=-3, iyon ay (0;0) at (-3;0) - dalawa pang puntos sa graph. Ang punto (o; 0) ay ang punto rin ng intersection ng parabola na may ordinate axis.
Sa x=1 y=-1²-3∙1=-4, iyon ay (1; -4) ay isang karagdagang punto para sa pag-plot.

Ang paggawa ng parabola mula sa mga punto ay isang mas matrabahong pamamaraan kumpara sa una. Kung ang parabola ay hindi bumalandra sa Ox axis, higit pang mga karagdagang puntos ang kinakailangan.
Bago magpatuloy sa pagbuo ng mga graph ng quadratic functions ng form na y=ax²+bx+c, isaalang-alang natin ang pagbuo ng mga graph ng mga function gamit ang geometric transformations. Ito rin ay pinaka-maginhawang gumawa ng mga graph ng mga function ng anyong y=x²+c gamit ang isa sa mga pagbabagong ito—parallel na pagsasalin.
Kategorya: |