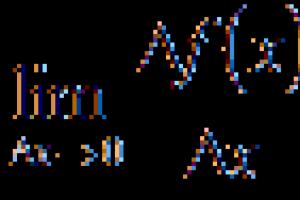Derivative ng exponential sa x power. Isang kamangha-manghang katangian ng derivative ng e sa kapangyarihan ng x Ano ang limitasyon

Patunay at derivation ng mga formula para sa derivative ng exponential (e sa x power) at exponential function (a sa x power). Mga halimbawa ng pagkalkula ng mga derivative ng e^2x, e^3x at e^nx. Mga formula para sa mga derivatives ng mas matataas na order.

Nilalaman

Tingnan din: Exponential function - mga katangian, formula, graph
Exponent, e sa x power - mga katangian, formula, graph

Mga pangunahing formula

Ang derivative ng isang exponent ay katumbas ng exponent mismo (ang derivative ng e sa x power ay katumbas ng e sa x power):
(1) (e x )′ = e x.

Ang derivative ng isang exponential function na may base a ay katumbas ng function mismo na pinarami ng natural na logarithm ng a:
(2) .

Ang exponential ay isang exponential function na ang base ay katumbas ng bilang e, na siyang sumusunod na limitasyon:
.
Dito maaari itong maging natural na numero o totoong numero. Susunod, nakukuha namin ang formula (1) para sa derivative ng exponential.

Derivation ng exponential derivative formula

Isaalang-alang ang exponential, e sa x power:
y = e x .
Ang function na ito ay tinukoy para sa lahat. Hanapin natin ang derivative nito patungkol sa variable na x. Sa pamamagitan ng kahulugan, ang derivative ay ang sumusunod na limitasyon:
(3) .

Ibahin natin ang ekspresyong ito upang bawasan ito sa mga kilalang katangian at panuntunan sa matematika. Upang gawin ito kailangan namin ang mga sumusunod na katotohanan:
A) Exponent property:
(4) ;
B) Katangian ng logarithm:
(5) ;
SA) Pagpapatuloy ng logarithm at pag-aari ng mga limitasyon para sa tuluy-tuloy na pag-andar:
(6) .
Narito ang isang function na may limitasyon at ang limitasyong ito ay positibo.
G) Ang kahulugan ng pangalawang kahanga-hangang limitasyon:
(7) .

Ilapat natin ang mga katotohanang ito sa ating limitasyon (3). Ginagamit namin ang ari-arian (4):
;
.

Gumawa tayo ng substitution. Pagkatapos ; .
Dahil sa pagpapatuloy ng exponential,
.
Samakatuwid, kapag , . Bilang resulta, nakukuha namin ang:
.

Gumawa tayo ng substitution. Tapos . Sa , . At mayroon kaming:
.

Ilapat natin ang logarithm property (5):
. Pagkatapos
.

Ilapat natin ang ari-arian (6). Dahil mayroong positibong limitasyon at ang logarithm ay tuloy-tuloy, kung gayon:
.
Dito rin namin ginamit ang pangalawang kapansin-pansing limitasyon (7). Pagkatapos
.

Kaya, nakuha namin ang formula (1) para sa derivative ng exponential.

Derivation ng formula para sa derivative ng isang exponential function

Ngayon ay nakukuha namin ang formula (2) para sa derivative ng exponential function na may base ng degree a. Naniniwala kami na at . Pagkatapos ay ang exponential function
(8)
Tinukoy para sa lahat.

Ibahin natin ang formula (8). Upang gawin ito, gagamitin namin ang mga katangian ng exponential function at logarithm.
;
.
Kaya, binago namin ang formula (8) sa sumusunod na anyo:
.

Higher order derivatives ng e sa x power

Ngayon, hanapin natin ang mga derivatives ng mas matataas na order. Tingnan muna natin ang exponent:
(14) .
(1) .

Nakikita natin na ang derivative ng function (14) ay katumbas ng function (14) mismo. Sa differentiating (1), nakakakuha tayo ng derivatives ng ikalawa at ikatlong order:
;
.

Ipinapakita nito na ang nth order derivative ay katumbas din ng orihinal na function:
.

Higher order derivatives ng exponential function

Ngayon isaalang-alang ang isang exponential function na may base ng degree a:
.
Natagpuan namin ang first-order derivative nito:
(15) .

Sa differentiating (15), nakakakuha tayo ng derivatives ng ikalawa at ikatlong order:
;
.

Nakikita namin na ang bawat pagkakaiba ay humahantong sa pagpaparami ng orihinal na function sa pamamagitan ng . Samakatuwid, ang nth order derivative ay may sumusunod na anyo:
.

Tingnan din:

Kapag hinango ang pinakaunang formula ng talahanayan, magpapatuloy tayo mula sa kahulugan ng derivative function sa isang punto. Dalhin natin kung saan x– anumang tunay na numero, iyon ay, x– anumang numero mula sa domain ng kahulugan ng function. Isulat natin ang limitasyon ng ratio ng increment ng function sa increment ng argument sa :

Dapat pansinin na sa ilalim ng limit sign ang expression ay nakuha, na hindi ang kawalan ng katiyakan ng zero na hinati ng zero, dahil ang numerator ay hindi naglalaman ng isang infinitesimal na halaga, ngunit tiyak na zero. Sa madaling salita, ang pagtaas ng isang pare-parehong pag-andar ay palaging zero.

kaya, derivative ng isang pare-parehong functionay katumbas ng zero sa buong domain ng kahulugan.

Derivative ng isang power function.

Ang formula para sa derivative ng isang power function ay may anyo , kung saan ang exponent p– anumang tunay na numero.

Patunayan muna natin ang formula para sa natural na exponent, iyon ay, para sa p = 1, 2, 3, …

Gagamitin natin ang kahulugan ng derivative. Isulat natin ang limitasyon ng ratio ng pagtaas ng isang function ng kapangyarihan sa pagtaas ng argumento:

Upang gawing simple ang expression sa numerator, bumaling tayo sa Newton binomial formula:

Kaya naman,

Pinatutunayan nito ang formula para sa derivative ng isang power function para sa isang natural na exponent.

Derivative ng isang exponential function.

Ipinakita namin ang derivation ng derivative formula batay sa kahulugan:

Dumating kami sa kawalan ng katiyakan. Upang palawakin ito, ipinakilala namin ang isang bagong variable, at sa . Tapos . Sa huling paglipat, ginamit namin ang formula para sa paglipat sa isang bagong logarithmic base.

Palitan natin ang orihinal na limitasyon:

Kung naaalala natin ang pangalawang kapansin-pansin na limitasyon, dumating tayo sa formula para sa derivative ng exponential function:

Derivative ng isang logarithmic function.

Patunayan natin ang formula para sa derivative ng isang logarithmic function para sa lahat x mula sa domain ng kahulugan at lahat ng wastong halaga ng base a logarithm Sa pamamagitan ng kahulugan ng derivative mayroon kaming:

Tulad ng napansin mo, sa panahon ng patunay ang mga pagbabago ay isinagawa gamit ang mga katangian ng logarithm. Pagkakapantay-pantay ay totoo dahil sa pangalawang kahanga-hangang limitasyon.

Mga derivative ng trigonometriko function.

Upang makakuha ng mga formula para sa mga derivatives ng trigonometriko function, kailangan nating alalahanin ang ilang mga formula ng trigonometry, pati na rin ang unang kapansin-pansin na limitasyon.

Sa pamamagitan ng kahulugan ng derivative para sa sine function na mayroon tayo .

Gamitin natin ang pagkakaiba ng sinus formula:

Ito ay nananatiling lumiko sa unang kapansin-pansing limitasyon:

Kaya, ang derivative ng function kasalanan x meron kasi x.

Ang formula para sa derivative ng cosine ay napatunayan sa eksaktong parehong paraan.

Samakatuwid, ang derivative ng function kasi x meron – kasalanan x.

Magkukuha tayo ng mga formula para sa talahanayan ng mga derivatives para sa tangent at cotangent gamit ang mga napatunayang panuntunan ng pagkita ng kaibhan (derivative ng isang fraction).

Mga derivative ng hyperbolic function.

Ang mga patakaran ng pagkita ng kaibhan at ang pormula para sa derivative ng exponential function mula sa talahanayan ng mga derivatives ay nagbibigay-daan sa amin upang makakuha ng mga formula para sa mga derivatives ng hyperbolic sine, cosine, tangent at cotangent.

Derivative ng inverse function.

Upang maiwasan ang pagkalito sa panahon ng pagtatanghal, tukuyin natin sa subscript ang argumento ng function kung saan isinasagawa ang pagkita ng kaibhan, iyon ay, ito ay ang derivative ng function. f(x) Sa pamamagitan ng x.

Ngayon ay magbalangkas tayo panuntunan para sa paghahanap ng derivative ng isang inverse function.

Hayaan ang mga function y = f(x) At x = g(y) magkabaligtaran, tinukoy sa pagitan at ayon sa pagkakabanggit. Kung sa isang punto ay mayroong isang finite non-zero derivative ng function f(x), pagkatapos ay sa puntong mayroong isang finite derivative ng inverse function g(y), at . Sa ibang post .

Maaaring baguhin ang panuntunang ito para sa alinman x mula sa pagitan , pagkatapos ay makuha namin .

Suriin natin ang bisa ng mga formula na ito.

Hanapin natin ang inverse function para sa natural na logarithm (Dito y ay isang function, at x- argumento). Ang pagkakaroon ng lutasin ang equation na ito para sa x, nakukuha natin (dito x ay isang function, at y- ang kanyang argumento). Yan ay, at magkabaligtaran na mga pag-andar.

Mula sa talahanayan ng mga derivatives makikita natin iyon At .

Siguraduhin natin na ang mga formula para sa paghahanap ng mga derivatives ng inverse function ay magdadala sa atin sa parehong mga resulta:

Nagpapakita kami ng talahanayan ng buod para sa kaginhawahan at kalinawan kapag pinag-aaralan ang paksa.

pare-parehoy = C Power function y = x p (x p) " = p x p - 1	Exponential functiony = isang x (a x) " = a x ln a Sa partikular, kapaga = emeron kami y = e x (e x) " = e x
Logarithmic function (log a x) " = 1 x ln a Sa partikular, kapaga = emeron kami y = log x (ln x) " = 1 x	Trigonometric function (sin x) " = cos x (cos x) " = - sin x (t g x) " = 1 cos 2 x (c t g x) " = - 1 sin 2 x
Inverse trigonometriko function (a r c sin x) " = 1 1 - x 2 (a r c cos x) " = - 1 1 - x 2 (a r c t g x) " = 1 1 + x 2 (a r c c t g x) " = - 1 1 + x 2	Hyperbolic function (s h x) " = c h x (c h x) " = s h x (t h x) " = 1 c h 2 x (c t h x) " = - 1 s h 2 x

Suriin natin kung paano nakuha ang mga formula ng tinukoy na talahanayan o, sa madaling salita, patunayan natin ang derivative na mga formula para sa bawat uri ng function.

Derivative ng isang pare-pareho

Katibayan 1

Upang makuha ang formula na ito, isinasaalang-alang namin bilang batayan ang kahulugan ng derivative ng isang function sa isang punto. Ginagamit namin ang x 0 = x, kung saan x kinukuha ang halaga ng anumang tunay na numero, o, sa madaling salita, x ay anumang numero mula sa domain ng function na f (x) = C. Isulat natin ang limitasyon ng ratio ng pagtaas ng isang function sa pagtaas ng argument bilang ∆ x → 0:

lim ∆ x → 0 ∆ f (x) ∆ x = lim ∆ x → 0 C - C ∆ x = lim ∆ x → 0 0 ∆ x = 0

Pakitandaan na ang expression na 0 ∆ x ay nasa ilalim ng limit sign. Hindi ito ang kawalan ng katiyakan na "zero na hinati ng zero," dahil ang numerator ay hindi naglalaman ng isang infinitesimal na halaga, ngunit tiyak na zero. Sa madaling salita, ang pagtaas ng isang pare-parehong pag-andar ay palaging zero.

Kaya, ang derivative ng constant function f (x) = C ay katumbas ng zero sa buong domain ng kahulugan.

Halimbawa 1

Ang mga pare-parehong pag-andar ay ibinibigay:

f 1 (x) = 3, f 2 (x) = a, a ∈ R, f 3 (x) = 4. 13 7 22 , f 4 (x) = 0 , f 5 (x) = - 8 7

Solusyon

Ilarawan natin ang mga ibinigay na kondisyon. Sa unang function nakita natin ang derivative ng natural na numero 3. Sa sumusunod na halimbawa, kailangan mong kunin ang derivative ng A, Saan A- anumang tunay na numero. Ang pangatlong halimbawa ay nagbibigay sa atin ng derivative ng hindi makatwirang numero 4. 13 7 22, ang pang-apat ay ang derivative ng zero (zero ay isang integer). Sa wakas, sa ikalimang kaso mayroon tayong derivative ng rational fraction - 8 7.

Sagot: derivatives ng mga ibinigay na function ay zero para sa anumang real x(sa buong lugar ng kahulugan)

f 1 " (x) = (3) " = 0 , f 2 " (x) = (a) " = 0 , a ∈ R , f 3 " (x) = 4 . 13 7 22 " = 0 , f 4 " (x) = 0 " = 0 , f 5 " (x) = - 8 7 " = 0

Derivative ng isang power function

Lumipat tayo sa power function at ang formula para sa derivative nito, na may anyo: (x p) " = p x p - 1, kung saan ang exponent p ay anumang tunay na numero.

Katibayan 2

Narito ang patunay ng formula kapag ang exponent ay isang natural na numero: p = 1, 2, 3, …

Muli tayong umaasa sa kahulugan ng isang derivative. Isulat natin ang limitasyon ng ratio ng pagtaas ng isang function ng kapangyarihan sa pagtaas ng argumento:

(x p) " = lim ∆ x → 0 = ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x) p - x p ∆ x

Upang gawing simple ang expression sa numerator, ginagamit namin ang binomial formula ng Newton:

(x + ∆ x) p - x p = C p 0 + x p + C p 1 · x p - 1 · ∆ x + C p 2 · x p - 2 · (∆ x) 2 + . . . + + C p p - 1 x (∆ x) p - 1 + C p p (∆ x) p - x p = = C p 1 x p - 1 ∆ x + C p 2 x p - 2 (∆ x) 2 + . . . + C p p - 1 x (∆ x) p - 1 + C p p (∆ x) p

kaya:

(x p) " = lim ∆ x → 0 ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x) p - x p ∆ x = = lim ∆ x → 0 (C p 1 x p - 1 ∆ x + C p 2 x p - 2 (∆ x) 2 + ... + C p p - 1 x (∆ x) p - 1 + C p p (∆ x) p) ∆ x = = lim ∆ x → 0 (C p 1 x p - 1 + C p 2 x p - 2 ∆ x + . . + C p p - 1 x (∆ x) p - 2 + C p p (∆ x) p - 1) = = C p 1 · x p - 1 + 0 + 0 + . . . + 0 = p ! 1 ! · (p - 1) ! · x p - 1 = p · x p - 1

Kaya, napatunayan namin ang formula para sa derivative ng isang power function kapag ang exponent ay isang natural na numero.

Katibayan 3

Upang magbigay ng ebidensya para sa kaso kung kailan p- anumang tunay na numero maliban sa zero, ginagamit namin ang logarithmic derivative (dito dapat nating maunawaan ang pagkakaiba mula sa derivative ng isang logarithmic function). Upang magkaroon ng mas kumpletong pag-unawa, ipinapayong pag-aralan ang derivative ng isang logarithmic function at higit na maunawaan ang derivative ng implicit function at ang derivative ng complex function.

Isaalang-alang natin ang dalawang kaso: kailan x positibo at kailan x negatibo.

Kaya x > 0. Pagkatapos: x p > 0 . Let us logarithm the equality y = x p to base e at ilapat ang property ng logarithm:

y = x p ln y = ln x p ln y = p · ln x

Sa yugtong ito, nakakuha kami ng isang tiyak na tinukoy na function. Tukuyin natin ang derivative nito:

(ln y) " = (p · ln x) 1 y · y " = p · 1 x ⇒ y " = p · y x = p · x p x = p · x p - 1

Ngayon ay isinasaalang-alang namin ang kaso kung kailan x – isang negatibong numero.

Kung ang indicator p ay isang even na numero, pagkatapos ay tinukoy ang power function para sa x< 0 , причем является четной: y (x) = - y ((- x) p) " = - p · (- x) p - 1 · (- x) " = = p · (- x) p - 1 = p · x p - 1

Pagkatapos x p< 0 и возможно составить доказательство, используя логарифмическую производную.

Kung p ay isang kakaibang numero, pagkatapos ay tinukoy ang power function para sa x< 0 , причем является нечетной: y (x) = - y (- x) = - (- x) p . Тогда x p < 0 , а значит логарифмическую производную задействовать нельзя. В такой ситуации возможно взять за основу доказательства правила дифференцирования и правило нахождения производной сложной функции:

y " (x) = (- (- x) p) " = - ((- x) p) " = - p · (- x) p - 1 · (- x) " = = p · (- x) p - 1 = p x p - 1

Ang huling paglipat ay posible dahil sa ang katunayan na kung p ay isang kakaibang numero, kung gayon p - 1 alinman sa kahit na numero o zero (para sa p = 1), samakatuwid, para sa negatibo x ang pagkakapantay-pantay (- x) p - 1 = x p - 1 ay totoo.

Kaya, napatunayan namin ang formula para sa derivative ng isang power function para sa anumang tunay na p.

Halimbawa 2

Mga ibinigay na function:

f 1 (x) = 1 x 2 3 , f 2 (x) = x 2 - 1 4 , f 3 (x) = 1 x log 7 12

Tukuyin ang kanilang mga derivatives.

Solusyon

Binabago namin ang ilan sa mga ibinigay na function sa tabular form y = x p , batay sa mga katangian ng degree, at pagkatapos ay gamitin ang formula:

f 1 (x) = 1 x 2 3 = x - 2 3 ⇒ f 1 " (x) = - 2 3 x - 2 3 - 1 = - 2 3 x - 5 3 f 2 " (x) = x 2 - 1 4 = 2 - 1 4 x 2 - 1 4 - 1 = 2 - 1 4 x 2 - 5 4 f 3 (x) = 1 x log 7 12 = x - log 7 12 ⇒ f 3" ( x) = - log 7 12 x - log 7 12 - 1 = - log 7 12 x - log 7 12 - log 7 7 = - log 7 12 x - log 7 84

Derivative ng isang exponential function

Patunay 4

Kunin natin ang derivative formula gamit ang kahulugan bilang batayan:

(a x) " = lim ∆ x → 0 a x + ∆ x - a x ∆ x = lim ∆ x → 0 a x (a ∆ x - 1) ∆ x = a x lim ∆ x → 0 a ∆ x - 1 ∆ x = 0 0

Nagkaroon kami ng kawalan ng katiyakan. Upang palawakin ito, magsulat tayo ng bagong variable z = a ∆ x - 1 (z → 0 bilang ∆ x → 0). Sa kasong ito, a ∆ x = z + 1 ⇒ ∆ x = log a (z + 1) = ln (z + 1) ln a . Para sa huling paglipat, ginamit ang formula para sa paglipat sa isang bagong logarithm base.

Palitan natin ang orihinal na limitasyon:

(a x) " = a x · lim ∆ x → 0 a ∆ x - 1 ∆ x = a x · ln a · lim ∆ x → 0 1 1 z · ln (z + 1) = = a x · ln a · lim ∆ x → 0 1 ln (z + 1) 1 z = a x · ln a · 1 ln lim ∆ x → 0 (z + 1) 1 z

Tandaan natin ang pangalawang kahanga-hangang limitasyon at pagkatapos ay makuha natin ang formula para sa derivative ng exponential function:

(a x) " = a x · ln a · 1 ln lim z → 0 (z + 1) 1 z = a x · ln a · 1 ln e = a x · ln a

Halimbawa 3

Ang mga exponential function ay ibinibigay:

f 1 (x) = 2 3 x , f 2 (x) = 5 3 x , f 3 (x) = 1 (e) x

Ito ay kinakailangan upang mahanap ang kanilang mga derivatives.

Solusyon

Ginagamit namin ang formula para sa derivative ng exponential function at ang mga katangian ng logarithm:

f 1 " (x) = 2 3 x " = 2 3 x ln 2 3 = 2 3 x (ln 2 - ln 3) f 2 " (x) = 5 3 x " = 5 3 x ln 5 1 3 = 1 3 5 3 x ln 5 f 3 " (x) = 1 (e) x " = 1 e x " = 1 e x ln 1 e = 1 e x ln e - 1 = - 1 e x

Derivative ng isang logarithmic function

Katibayan 5

Magbigay tayo ng patunay ng formula para sa derivative ng isang logarithmic function para sa alinman x sa domain ng kahulugan at anumang pinahihintulutang halaga ng base a ng logarithm. Batay sa kahulugan ng derivative, nakukuha natin ang:

(log a x) " = lim ∆ x → 0 log a (x + ∆ x) - log a x ∆ x = lim ∆ x → 0 log a x + ∆ x x ∆ x = = lim ∆ x → 0 1 ∆ x log a 1 + ∆ x x = lim ∆ x → 0 log a 1 + ∆ x x 1 ∆ x = = lim ∆ x → 0 log a 1 + ∆ x x 1 ∆ x · x x = lim ∆ x → 0 1 x · log a 1 + ∆ x x x ∆ x = = 1 x · log a lim ∆ x → 0 1 + ∆ x x x ∆ x = 1 x · log a e = 1 x · ln e ln a = 1 x · ln a

Mula sa ipinahiwatig na kadena ng mga pagkakapantay-pantay ay malinaw na ang mga pagbabagong-anyo ay batay sa pag-aari ng logarithm. Ang equality lim ∆ x → 0 1 + ∆ x x x ∆ x = e ay totoo alinsunod sa pangalawang kapansin-pansing limitasyon.

Halimbawa 4

Ang mga function ng logarithmic ay ibinibigay:

f 1 (x) = log ln 3 x , f 2 (x) = ln x

Ito ay kinakailangan upang kalkulahin ang kanilang mga derivatives.

Solusyon

Ilapat natin ang nagmula na formula:

f 1 " (x) = (log ln 3 x) " = 1 x · ln (ln 3) ; f 2 " (x) = (ln x) " = 1 x ln e = 1 x

Kaya, ang derivative ng natural logarithm ay isa na hinati ng x.

Mga derivative ng trigonometriko function

Patunay 6

Gumamit tayo ng ilang trigonometric formula at ang unang kahanga-hangang limitasyon upang makuha ang formula para sa derivative ng isang trigonometric function.

Ayon sa kahulugan ng derivative ng sine function, nakukuha natin:

(sin x) " = lim ∆ x → 0 sin (x + ∆ x) - sin x ∆ x

Ang formula para sa pagkakaiba ng mga sine ay magbibigay-daan sa amin upang maisagawa ang mga sumusunod na aksyon:

(sin x) " = lim ∆ x → 0 sin (x + ∆ x) - sin x ∆ x = = lim ∆ x → 0 2 sin x + ∆ x - x 2 cos x + ∆ x + x 2 ∆ x = = lim ∆ x → 0 sin ∆ x 2 · cos x + ∆ x 2 ∆ x 2 = = cos x + 0 2 · lim ∆ x → 0 sin ∆ x 2 ∆ x 2

Sa wakas, ginagamit namin ang unang kahanga-hangang limitasyon:

kasalanan " x = cos x + 0 2 · lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = cos x

Kaya, ang derivative ng function kasalanan x kalooban kasi x.

Patunayan din natin ang formula para sa derivative ng cosine:

cos " x = lim ∆ x → 0 cos (x + ∆ x) - cos x ∆ x = = lim ∆ x → 0 - 2 sin x + ∆ x - x 2 sin x + ∆ x + x 2 ∆ x = = - lim ∆ x → 0 sin ∆ x 2 sin x + ∆ x 2 ∆ x 2 = = - sin x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = - sin x

Yung. ang derivative ng cos x function ay magiging – kasalanan x.

Nakukuha namin ang mga formula para sa mga derivatives ng tangent at cotangent batay sa mga patakaran ng pagkita ng kaibhan:

t g " x = sin x cos x " = sin " x · cos x - sin x · cos " x cos 2 x = = cos x · cos x - sin x · (- sin x) cos 2 x = sin 2 x + cos 2 x cos 2 x = 1 cos 2 x c t g " x = cos x sin x " = cos " x · sin x - cos x · sin " x sin 2 x = = - sin x · sin x - cos x · cos x sin 2 x = - sin 2 x + cos 2 x sin 2 x = - 1 sin 2 x

Derivatives ng inverse trigonometriko function

Ang seksyon sa derivative ng inverse functions ay nagbibigay ng komprehensibong impormasyon sa patunay ng mga formula para sa mga derivatives ng arcsine, arccosine, arctangent at arccotangent, kaya hindi namin duplicate ang materyal dito.

Mga derivative ng hyperbolic function

Katibayan 7

Maaari nating makuha ang mga formula para sa mga derivative ng hyperbolic sine, cosine, tangent at cotangent gamit ang differentiation rule at ang formula para sa derivative ng exponential function:

s h " x = e x - e - x 2 " = 1 2 e x " - e - x " = = 1 2 e x - - e - x = e x + e - x 2 = c h x c h " x = e x + e - x 2 " = 1 2 e x " + e - x " = = 1 2 e x + - e - x = e x - e - x 2 = s h x t h " x = s h x c h x " = s h " x · c h x - s h x · c h " x c h 2 x = c h 2 x - s h 2 x c h 2 x = 1 c h 2 x c t h " x = c h x s h x " = c h " x · s h x - c h x · s h " x s h 2 x = s h 2 x - c h 2 x s h 2 x = - 1 s h 2 x

Kung may napansin kang error sa text, paki-highlight ito at pindutin ang Ctrl+Enter

Maraming mga numero ang nakakuha ng kanilang magnitude at mapamahiin na kahulugan noong sinaunang panahon. Sa ngayon, ang mga bagong alamat ay idinaragdag sa kanila. Mayroong maraming mga alamat tungkol sa numerong pi; ang mga sikat na numero ng Fibonacci ay hindi gaanong sikat kaysa dito. Ngunit marahil ang pinaka nakakagulat na bagay ay ang numero e, na hindi niya magagawa kung wala modernong matematika, pisika at maging sa ekonomiya.

Ang arithmetic value ng e ay humigit-kumulang 2.718. Bakit hindi eksakto, ngunit humigit-kumulang? Dahil ang numerong ito ay hindi makatwiran at transendental, hindi ito maaaring ipahayag bilang isang fraction na may natural na integer o isang polynomial na may rational coefficients. Para sa karamihan ng mga kalkulasyon, sapat na ang tinukoy na katumpakan ng 2.718, bagama't ang modernong antas ng teknolohiya sa pag-compute ay nagpapahintulot sa halaga nito na matukoy nang may katumpakan na higit sa isang trilyong decimal na lugar.

Ang pangunahing tampok ng numerong e ay ang derivative ng exponential function nito f (x) = e x ay katumbas ng halaga ng function na e x mismo. Walang ibang mathematical na relasyon ang may ganitong kakaibang katangian. Pag-usapan natin ito nang mas detalyado.

Ano ang limitasyon

Una, unawain natin ang konsepto ng limitasyon. Isaalang-alang ang ilang mathematical expression, halimbawa, i = 1/n. Maaaring makita, na habang tumataas ang “n”.", bababa ang halaga ng "i", at dahil ang "n" ay may posibilidad na infinity (na ipinapahiwatig ng sign ∞), ang "i" ay may posibilidad na limitahan ang halaga (mas madalas na tinatawag na limitasyon) na katumbas ng zero. Ang expression para sa limitasyon (na tinukoy bilang lim) para sa kaso na isinasaalang-alang ay maaaring isulat bilang lim n →∞ (1/ n) = 0.

Mayroong iba't ibang mga limitasyon para sa iba't ibang mga expression. Ang isa sa mga limitasyong ito, kasama sa mga aklat-aralin ng Sobyet at Ruso bilang pangalawang kapansin-pansing limitasyon, ay ang ekspresyong lim n →∞ (1+1/ n) n. Nasa Middle Ages na ito ay itinatag na ang limitasyon ng expression na ito ay ang bilang e.

Kasama sa unang kapansin-pansing limitasyon ang expression na lim n →∞ (Sin n / n) = 1.

Paano hanapin ang derivative ng e x - sa video na ito.

Ano ang derivative ng isang function

Upang ipaliwanag ang konsepto ng isang derivative, dapat nating alalahanin kung ano ang isang function sa matematika. Upang hindi kalat ang teksto ng mga kumplikadong kahulugan, tututuon natin ang intuitive na konsepto ng matematika ng isang function, na binubuo sa katotohanan na sa loob nito ay ganap na tinutukoy ng isa o higit pang mga dami ang halaga ng isa pang dami kung magkakaugnay ang mga ito. Halimbawa, sa formula S = π ∙ r 2 ang lugar ng isang bilog, ang halaga ng radius r ay ganap at natatanging tinutukoy ang lugar ng bilog S.

Depende sa uri, ang mga function ay maaaring algebraic, trigonometriko, logarithmic, atbp. Maaari silang magkaroon ng dalawa, tatlo o higit pang argument na magkakaugnay. Halimbawa, ang distansya na nilakbay ng S, kung saan ang isang bagay na sakop sa isang pare-parehong pinabilis na bilis, ay inilalarawan ng function na S = 0.5 ∙ a ∙ t 2 + V ∙ t, kung saan ang “t” ay ang oras ng paggalaw, ang argumentong “a ” ay acceleration (maaaring maging positibo o at negatibong halaga) at ang “V” ay ang paunang bilis ng paggalaw. Kaya, ang distansya na nilakbay ay nakasalalay sa mga halaga ng tatlong argumento, dalawa sa mga ito ("a" at "V") ay pare-pareho.

Gamitin natin ang halimbawang ito upang ipakita ang elementarya na konsepto ng isang derivative ng isang function. Inilalarawan nito ang rate ng pagbabago ng function sa isang naibigay na punto. Sa aming halimbawa, ito ang magiging bilis ng paggalaw ng bagay sa isang tiyak na sandali sa oras. Sa patuloy na "a" at "V", nakasalalay lamang ito sa oras na "t", iyon ay, sa wikang pang-agham, kailangan mong kunin ang derivative ng function na S na may paggalang sa oras na "t".

Ang prosesong ito ay tinatawag na pagkita ng kaibhan at ginagawa sa pamamagitan ng pagkalkula ng limitasyon ng ratio ng paglago ng isang function sa paglago ng argumento nito sa pamamagitan ng isang hindi gaanong maliit na halaga. Ang paglutas ng mga naturang problema para sa mga indibidwal na function ay kadalasang mahirap at hindi tinatalakay dito. Nararapat ding tandaan na ang ilang mga pag-andar sa ilang mga punto ay walang ganoong limitasyon.

Sa aming halimbawa, ang derivative na S Sa paglipas ng panahon, ang "t" ay magkakaroon ng anyong S" = ds/dt = a ∙ t + V, kung saan makikita na ang bilis ng S" ay nagbabago ayon sa isang linear na batas depende sa "t".

Derivative ng exponent

Ang exponential function ay tinatawag na exponential function, ang base nito ay ang numerong e. Karaniwan itong ipinapakita sa form na F (x) = e x, kung saan ang exponent x ay variable na dami. Ang function na ito ay may kumpletong pagkakaiba-iba sa buong hanay ng mga tunay na numero. Habang lumalaki ang x, patuloy itong tumataas at palaging mas malaki kaysa sa zero. Ang inverse function nito ay ang logarithm.

Nagawa ng sikat na matematiko na si Taylor na palawakin ang function na ito sa isang serye na ipinangalan sa kanya e x = 1 + x/1! + x 2/2! + x 3/3! + … sa hanay ng x mula - ∞ hanggang + ∞.

Batas batay sa tungkuling ito, ay tinatawag na exponential. Inilalarawan niya:

• pagtaas ng mga rate ng interes ng tambalang bangko;
• pagtaas ng populasyon ng hayop at pandaigdigang populasyon;
• rigor mortis time at marami pang iba.

Ulitin natin muli ang kahanga-hangang pag-aari ng dependence na ito - ang halaga ng derivative nito sa anumang punto ay palaging katumbas ng halaga ng function sa puntong ito, iyon ay, (e x)" = e x.

Ipakita natin ang mga derivative para sa pinaka-pangkalahatang mga kaso ng exponential:

• (e ax)" = a ∙ e ax;
• (e f (x))" = f"(x) ∙ e f (x) .

Gamit ang mga dependency na ito, madaling makahanap ng mga derivatives para sa iba pang partikular na uri ng function na ito.

Ilang kawili-wiling katotohanan tungkol sa numero e

Ang mga pangalan ng naturang mga siyentipiko tulad ng Napier, Oughtred, Huygens, Bernoulli, Leibniz, Newton, Euler, at iba pa ay nauugnay sa numerong ito. Talagang ipinakilala ng huli ang notasyong e para sa numerong ito, at natagpuan din ang unang 18 palatandaan, gamit ang seryeng e = 1 + 1/1 na natuklasan niya para sa pagkalkula! + 2/2! + 3/3! ...

Lumilitaw ang numerong e sa mga hindi inaasahang lugar. Halimbawa, ito ay kasama sa catenary equation, na naglalarawan sa sag ng isang lubid sa ilalim ng sarili nitong timbang kapag ang mga dulo nito ay naayos sa mga suporta.

Video

Ang paksa ng aralin sa video ay ang derivative ng exponential function.

Pangunahing Konsepto

Bago suriin ang tanong ng derivative ng exponential sa kapangyarihan $x$, alalahanin natin ang mga kahulugan

1. mga function;
2. limitasyon ng pagkakasunud-sunod;
3. derivative;
4. mga exhibitors.

Ito ay kinakailangan para sa isang malinaw na pag-unawa sa derivative ng isang exponential sa kapangyarihan ng $x$.

Kahulugan 1

Ang function ay isang relasyon sa pagitan ng dalawang variable.

Kunin natin ang $y=f(x)$, kung saan ang $x$ at $y$ ay mga variable. Dito ang $x$ ay tinatawag na argument at $y$ ang function. Ang argument ay maaaring tumagal ng mga arbitrary na halaga. Sa turn, ang variable na $y$ ay nagbabago ayon sa isang partikular na batas depende sa argumento. Ibig sabihin, ang argument na $x$ ay ang independent variable, at ang function na $y$ ay ang dependent variable. Para sa anumang halaga na $x$ mayroong natatanging halaga na $y$.

Kung, sa bisa ng ilang batas, ang bawat natural na bilang na $n=1, 2, 3, ...$ ay nauugnay sa isang numerong $x_n$, pagkatapos ay sinasabi namin na ang pagkakasunod-sunod ng mga numerong $x_1,x_2,..., x_n$ ay tinukoy. Kung hindi, ang ganitong pagkakasunod-sunod ay isinulat bilang $\(x_n\)$. Ang lahat ng mga numerong $x_n$ ay tinatawag na mga miyembro o elemento ng sequence.

Kahulugan 2

Ang limitasyon ng isang sequence ay ang may hangganan o walang katapusan na malayong punto ng linya ng numero. Ang limitasyon ay nakasulat tulad ng sumusunod: $\lim x_n = \lim\limits_(n\to\infty)x_n = a$. Ang notasyong ito ay nangangahulugan na ang variable na $x_n$ ay may posibilidad na $a$ $x_n\to a$.

Ang derivative ng function na $f$ sa puntong $x_0$ ay tinatawag na sumusunod na limitasyon:

$\lim\limits_(x\to x_0)\frac(f(x) - f(x_o))(x-x_o)$. Ito ay tinutukoy ng $f"(x_0)$.

Ang bilang na $e$ ay katumbas ng sumusunod na limitasyon:

$e=\lim\limits_(x\to\infty) (1+\frac(1)(n))\approx2.718281828459045...$

Sa limitasyong ito, ang $n$ ay natural o totoong numero.

Sa pagkakaroon ng mastered sa mga konsepto ng limit, derivative at exponent, maaari nating simulan na patunayan ang formula na $(e^x)"=e^x$.

Derivation ng derivative ng exponential sa power $x$

Mayroon kaming $e^x$, kung saan $x: -\infty

$y"=\lim\limits_(\Delta x\to 0) \frac(e^(x+\Delta x)-e^x)(\Delta x)$.

Sa pamamagitan ng pag-aari ng exponent na $e^(a+bx)=e^a*e^b$ maaari nating baguhin ang numerator ng limitasyon:

$e^(x+\Delta x)-e^x = e^x*e^(\Delta x)-e^x = e^x(e^(\Delta x)-1)$.

Ibig sabihin, $y"=\lim\limits_(\Delta x\to 0) \frac(e^(x+\Delta x)-e^x)(\Delta x)=\lim\limits_(\Delta x\ hanggang 0) \frac(e^x(e^(\Delta x)-1))(\Delta x)$.

Tukuyin natin ang $t=e^(\Delta x)-1$. Nakukuha namin ang $e^(\Delta x)=t+1$, at sa pamamagitan ng property ng logarithm lumalabas na $\Delta x = ln(t+1)$.

Dahil tuloy-tuloy ang exponential, mayroon kaming $\lim\limits_(\Delta x\to 0) e^(\Delta x)=e^0=1.$ Samakatuwid, kung $\Delta x\to 0$, kung gayon ay $ t \ hanggang 0$.

Bilang resulta, ipinapakita namin ang pagbabagong-anyo:

$y"=\lim\limits_(\Delta x\to 0) \frac(e^(\Delta x)-1)(\Delta x)=e^x\lim\limits_(t\to 0)\frac (t)(ln(t+1))$.

Tukuyin natin ang $n=\frac (1)(t)$, pagkatapos ay $t=\frac(1)(n)$. Lumalabas na kung $t\to 0$, $n\to\infty$.

Baguhin natin ang ating limitasyon:

$y"=e^x\lim\limits_(t\to 0)\frac(t)(ln(t+1))=e^x\lim\limits_(n\to\infty)\frac(1) (n\cdot ln(\frac(1)(n)+1)^n)$.

Sa pamamagitan ng pag-aari ng logarithm $b\cdot ln c=ln c^b$ mayroon tayo

$n\cdot ln (\frac(1)(n)+1)=ln(\frac(1)(n)+1)^n=ln(1+\frac(1)(n))^n$ .

Ang limitasyon ay na-convert bilang mga sumusunod:

$y"=e^x\lim\limits_(n\to\infty)\frac(1)(n\cdot ln(\frac(1)(n)+1)) = e^x\lim\limits_( n\to\infty)\frac(1)(ln(\frac(1)(n)+1)^n)= e^x\frac(1)(\lim\limits_(n\to\infty) ln (\frac(1)(n)+1)^n)$.

Ayon sa pag-aari ng pagpapatuloy ng logarithm at ang pag-aari ng mga limitasyon para sa isang tuluy-tuloy na function: $\lim\limits_(x\to x_0)ln(f(x))=ln(\lim\limits_f(x))$, kung saan ang $f(x)$ ay may positibong limitasyon $\lim\limits_(x\to x_0)f(x)$. Kaya, dahil sa ang katunayan na ang logarithm ay tuloy-tuloy at mayroong positibong limitasyon $\lim\limits_(n\to\infty)(\frac(1)(n)+1)^n$, maaari nating mahihinuha:

$\lim\limits_(n\to\infty)ln(1+\frac(1)(n))^n=ln\lim\limits_(n\to\infty)ln(1+\frac(1)( n))^n=ln e=1$.

Gamitin natin ang halaga ng pangalawang kahanga-hangang limitasyon $\lim\limits_(n\to\infty)(1+\frac(1)(n))^n=e$. Nakukuha namin:

$y"= e^x\frac(1)(\lim\limits_(n\to\infty) ln(\frac(1)(n)+1)^n) = e^x\cdot\frac(1 )(ln e) = e^x\cdot\frac(1)(1)=e^x$.

Kaya, nakuha namin ang formula para sa derivative ng isang exponential at maaaring i-claim na ang derivative ng exponential sa kapangyarihan ng $x$ ay katumbas ng derivative ng exponential sa kapangyarihan ng $x$:

Mayroon ding iba pang mga paraan upang makuha ang formula na ito gamit ang iba pang mga formula at panuntunan.

Halimbawa 1

Tingnan natin ang isang halimbawa ng paghahanap ng derivative ng isang function.

Kundisyon: Hanapin ang derivative ng function na $y=2^x + 3^x + 10^x + e^x$.

Solusyon: Sa mga terminong $2^x, 3^x$ at $10^x$ inilalapat namin ang formula na $(a^x)"=a^x\cdot ln a$. Ayon sa derived formula na $(e^x)" =e^x$ ang ikaapat na termino na $e^x$ ay hindi nagbabago.

Sagot: $y" = 2^x\cdot ln 2 + 3^x\cdot ln 3 + 10^x\cdot ln 10 + e^x$.

Kaya, nakuha namin ang formula na $(e^x)"=e^x$, habang nagbibigay ng mga kahulugan sa mga pangunahing konsepto, at sinuri ang isang halimbawa ng paghahanap ng derivative ng isang function na may exponent bilang isa sa mga termino.